|
Automatic track mixing
By using state-of-the-art algorithms for beat tracking and structure analysis, our goal is to create a continuous flow of music with seamless transitions between tracks.
The objective is a fully automated mixing system with focus on electronic dance music.
Contact: Mickaël Zehren
| 
Canonical Polyadic Tensor Decomposition
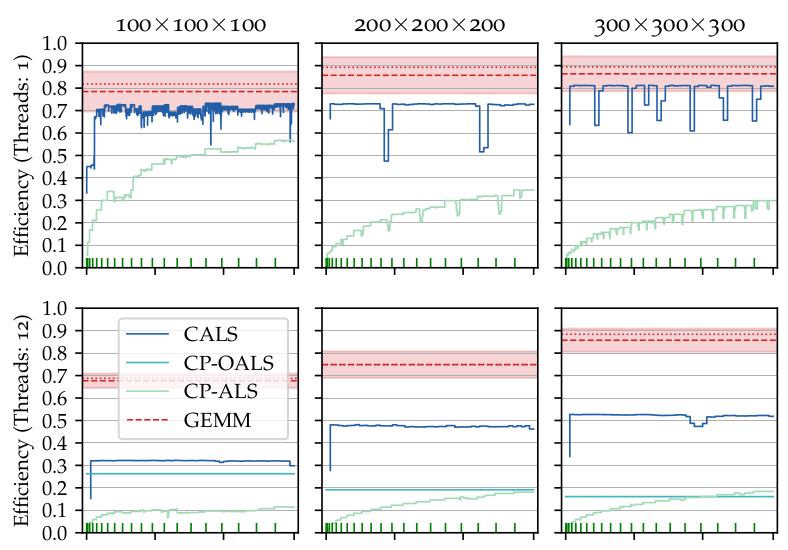
- Algorithm 1026: Concurrent Alternating Least Squares for multiple simultaneous Canonical Polyadic Decompositions
ACM Transactions on Mathematical Software, Volume 48(3), pp. 1-20, September 2022. @article{Psarras2022:980,
author = "Christos Psarras and Lars Karlsson and Rasmus Bro and Paolo Bientinesi",
title = "Algorithm 1026: Concurrent Alternating Least Squares for multiple simultaneous Canonical Polyadic Decompositions",
journal = "ACM Transactions on Mathematical Software",
year = 2022,
volume = 48,
number = 3,
pages = "1--20",
month = sep,
doi = "10.1145/3519383"
}Tensor decompositions, such as CANDECOMP/PARAFAC (CP), are widely used in a variety of applications, such as chemometrics, signal processing, and machine learning. A broadly used method for computing such decompositions relies on the Alternating Least Squares (ALS) algorithm. When the number of components is small, regardless of its implementation, ALS exhibits low arithmetic intensity, which severely hinders its performance and makes GPU offloading ineffective. We observe that, in practice, experts often have to compute multiple decompositions of the same tensor, each with a small number of components (typically fewer than 20), to ultimately find the best ones to use for the application at hand. In this paper, we illustrate how multiple decompositions of the same tensor can be fused together at the algorithmic level to increase the arithmetic intensity. Therefore, it becomes possible to make efficient use of GPUs for further speedups; at the same time the technique is compatible with many enhancements typically used in ALS, such as line search, extrapolation, and non-negativity constraints. We introduce the Concurrent ALS algorithm and library, which offers an interface to Matlab, and a mechanism to effectively deal with the issue that decompositions complete at different times. Experimental results on artificial and real datasets demonstrate a shorter time to completion due to increased arithmetic intensity. - Accelerating jackknife resampling for the Canonical Polyadic Decomposition
Frontiers in Applied Mathematics and Statistics, Volume 8, April 2022. @article{Psarras2022:328,
author = "Christos Psarras and Lars Karlsson and Rasmus Bro and Paolo Bientinesi",
title = "Accelerating jackknife resampling for the Canonical Polyadic Decomposition",
journal = "Frontiers in Applied Mathematics and Statistics",
year = 2022,
volume = 8,
month = apr,
doi = "10.3389/fams.2022.830270",
url = "https://www.frontiersin.org/articles/10.3389/fams.2022.830270/pdf"
}The Canonical Polyadic (CP) tensor decomposition is frequently used as a model in applications in a variety of different fields. Using jackknife resampling to estimate parameter uncertainties is often desirable but results in an increase of the already high computational cost. Upon observation that the resampled tensors, though different, are nearly identical, we show that it is possible to extend the recently proposed Concurrent ALS (CALS) technique to a jackknife resampling scenario. This extension gives access to the computational efficiency advantage of CALS for the price of a modest increase (typically a few percent) in the number of floating point operations. Numerical experiments on both synthetic and real-world datasets demonstrate that the new workflow based on a CALS extension can be several times faster than a straightforward workflow where the jackknife submodels are processed individually.
| | 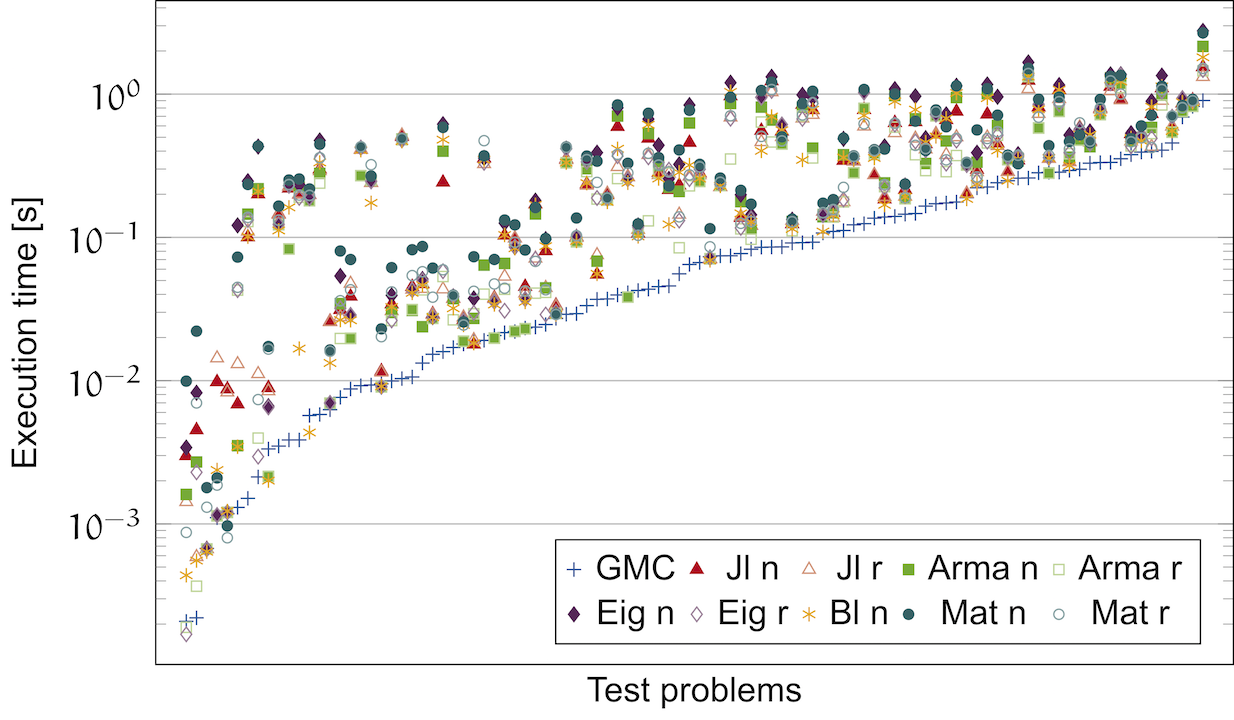
Linnea
The Generalized Matrix Chain (GMC) algorithm, which is part of Linnea, generates code that substantially outperforms high-level languages for linear algebra, as well as C++ expression template libraries.
The Generalized Matrix Chain Algorithm
Henrik Barthels, Marcin Copik and Paolo Bientinesi
| | 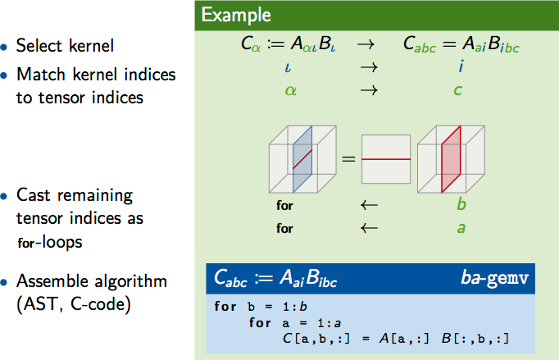
Algorithm Generation
yields hundreds of implementations for tensor contractions.
- On the Performance Prediction of BLAS-based Tensor Contractions
High Performance Computing Systems. Performance Modeling, Benchmarking, and Simulation, Lecture Notes in Computer Science, Volume 8966, pp. 193-212, Springer International Publishing, April 2015. @inproceedings{Peise2015:380,
author = "Elmar Peise and Diego Fabregat-Traver and Paolo Bientinesi",
title = "On the Performance Prediction of BLAS-based Tensor Contractions",
booktitle = "High Performance Computing Systems. Performance Modeling, Benchmarking, and Simulation",
year = 2015,
editor = "Jarvis, Stephen A. and Wright, Steven A. and Hammond, Simon D.",
volume = 8966,
series = "Lecture Notes in Computer Science",
pages = "193-212",
month = apr,
publisher = "Springer International Publishing",
doi = "10.1007/978-3-319-17248-4_10",
url = "http://arxiv.org/pdf/1409.8608v1"
}Tensor operations are surging as the computational building blocks for a variety of scientific simulations and the development of high-performance kernels for such operations is known to be a challenging task. While for operations on one- and two-dimensional tensors there exist standardized interfaces and highly-optimized libraries (BLAS), for higher dimensional tensors neither standards nor highly-tuned implementations exist yet. In this paper, we consider contractions between two tensors of arbitrary dimensionality and take on the challenge of generating high-performance implementations by resorting to sequences of BLAS kernels. The approach consists in breaking the contraction down into operations that only involve matrices or vectors. Since in general there are many alternative ways of decomposing a contraction, we are able to methodically derive a large family of algorithms. The main contribution of this paper is a systematic methodology to accurately identify the fastest algorithms in the bunch, without executing them. The goal is instead accomplished with the help of a set of cache-aware micro-benchmarks for the underlying BLAS kernels. The predictions we construct from such benchmarks allow us to reliably single out the best-performing algorithms in a tiny fraction of the time taken by the direct execution of the algorithms.
| 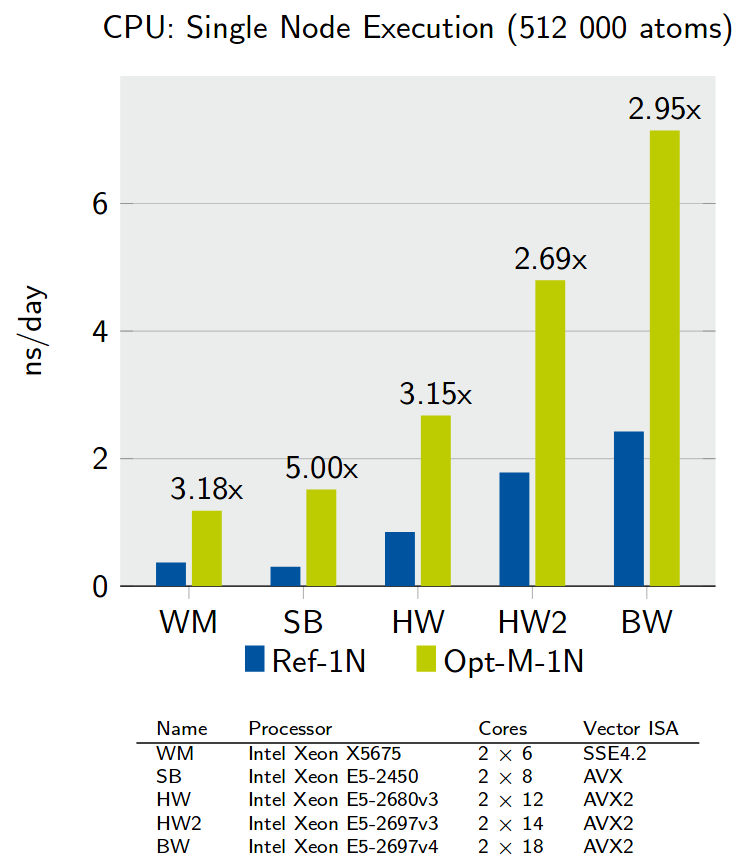
Many-Body Potential Optimization
Optimizing core many-body potentials for molecular dynamics simulations in materials science.
- Accelerating AIREBO: Navigating the Journey from Complex Legacy Code to High Performance
Journal of Computational Chemistry, Volume 40(14), May 2019. @article{Höhnerbach2019:708,
author = "Markus Höhnerbach and Paolo Bientinesi",
title = "Accelerating AIREBO: Navigating the Journey from Complex Legacy Code to High Performance",
journal = "Journal of Computational Chemistry",
year = 2019,
volume = 40,
number = 14,
month = may,
url = "https://arxiv.org/pdf/1810.07026.pdf"
}Despite initiatives to improve the quality of scientific codes, there still is a large presence of legacy code. Such code often needs to implement a lot of functionality under time constrains, sacrificing quality. Additionally, quality is rarely improved by optimizations for new architectures. This development model leads to code that is increasingly difficult to work with. Our suggested solution includes complexity-reducing refactoring and hardware abstraction. We focus on the AIREBO potential from LAMMPS, where the challenge is that any potential kernel is rather large and complex, hindering systematic optimization. This issue is common to codes that model multiple physical phenomena. We present our journey from the C++ port of a previous Fortran code to performance-portable, KNC-hybrid, vectorized, scalable, optimized code supporting full and reduced precision. The journey includes extensive testing that fixed bugs in the original code. Large-scale, full-precision runs sustain speedups of more than 4x (KNL) and 3x (Skylake). - The Vectorization of the Tersoff Multi-Body Potential: An Exercise in Performance Portability
Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC'16, Number 7, pp. 7:1-7:13, IEEE Press, 2016.
Selected for Reproducibility Initiative at SC17. @inproceedings{Höhnerbach2016:78,
author = "Markus Höhnerbach and {Ahmed E.} Ismail and Paolo Bientinesi",
title = "The Vectorization of the Tersoff Multi-Body Potential: An Exercise in Performance Portability",
booktitle = "Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis",
year = 2016,
number = 7,
series = "SC'16",
pages = "7:1--7:13",
publisher = "IEEE Press",
note = "Selected for Reproducibility Initiative at SC17",
url = "https://arxiv.org/pdf/1607.02904v1"
}Molecular dynamics simulations, an indispensable research tool in computational chemistry and materials science, consume a significant portion of the supercomputing cycles around the world. We focus on multi-body potentials and aim at achieving performance portability. Compared with well-studied pair potentials, multibody potentials deliver increased simulation accuracy but are too complex for effective compiler optimization. Because of this, achieving cross-platform performance remains an open question. By abstracting from target architecture and computing precision, we develop a vectorization scheme applicable to both CPUs and accelerators. We present results for the Tersoff potential within the molecular dynamics code LAMMPS on several architectures, demonstrating efficiency gains not only for computational kernels, but also for large-scale simulations. On a cluster of Intel Xeon Phi's, our optimized solver is between 3 and 5 times faster than the pure MPI reference.
|








