Automatic mixing

Dissonance suppression during harmonic mixing

A journey through the DJ world
by Stefan Hamburger
July 2017
Seminar Topics in Computer Music
Prof. Paolo Bientinesi, RWTH Aachen

2.1

What is automatic mixing?

Generating a continuous stream of music with smooth transitions

Track A → Track B

3.1

DJs in a club

DJing is the main application for automatic mixing. If you think about DJs in a club, their job is to play back the music and keep everyone entertained. The end of a song is the most critical time because if they choose a wrong follow-up song that the crowd doesn't like, the DJ risks clearing the dancefloor. The clubgoers may decide to stop dancing, get a drink or even leave the club which is bad for a DJ's reputation and career.

Therefore, when DJing became widespread in the late 60s and 70s with the rise of disco music, DJs had to quickly learn to improve their mixing.

3.2

History of DJing

Francis Grasso: beatmatching

Technics SL-1200 (1971)

One pioneer in the DJing field was Francis Grasso, a DJ from New York. He developed what is now known as beatmatching. As you heard in the previous talk on tempo adjustment, beatmatching means changing the speed so that the beats from both tracks align and people can keep dancing in the same rhythm.

For this, turntables have a slider on the side, allowing DJs to change the playback speed of a song. The problem with physical turntables is that changing the tempo automatically changes the pitch – if you compress a waveform, the frequency will go up.

The turntable shown in this image only allows a tempo change up to 8%, this ensures that you can't change the tempo so much that the song would sound too high- or low-pitched. For good beatmatching, DJs need to make sure that any follow-up song already has a tempo similar to the current song, else the mixing will fail.

Image source:
https://commons.wikimedia.org/wiki/File:Technics_SL-1200MK2-2.jpg
https://commons.wikimedia.org/wiki/File:Technics_SL-1210MK2_pitch_control.jpeg

3.3

History of DJing

1986: Harmonic Keys magazine (Stuart Soroka)

The need for a better song selection was recognized by Stuart Soroka, a DJ from Key West. In his Harmonic Keys magazine, he published the tempo and key information for the most popular tracks. Back then, DJs did not have a digital archive, instead they carried their vinyl tracks in a big box. Given the tempo and key information, they were able to sort their record collection at home, so that when they are playing in a club, they could easily find follow-up tracks that fit the current track and would guarantee a good mixing.

The Harmonic Keys magazine was very popular but two years later, it disappeared mysteriously. It is unknown what happened, maybe Stuart Soroka died, or he took the subscription money and ran; but fortunately this was not the end of harmonic mixing.

Image source: http://ultramaroon.net/category/harmonic-keys/

3.4

History of DJing

Camelot Sound (Mark Davis)

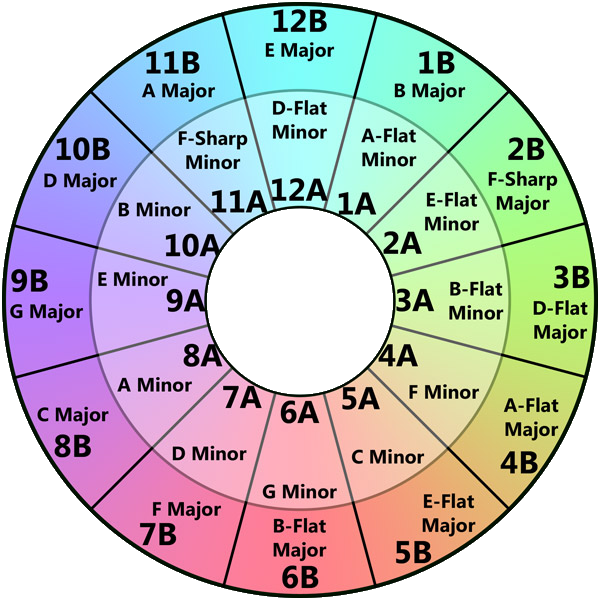
EasyMix wheel

Mark Davis, a DJ from California, continued the work after the Harmonic Keys magazine disappeared. At his company Camelot Sound, he built a database with tempo and key information of new music tracks as they came out.

Where the Harmonic Keys magazine required understanding the different keys (like that D minor is the dominant of G minor and therefore fits well together), Mark Davis simplified it. He understood that DJs are typically not musicians, so he invented the EasyMix wheel which is still in use today. On the EasyMix wheel, all keys are mapped onto the numbers from 1-12, so instead of D minor and G minor we now have 6A and 7A. Because these numbers are very similar (they're only off by one), a DJ knows that these two keys mix well together, whereas numbers that are far apart do not mix as nicely.

Image source: http://camelotsound.com/Easymix.aspx

3.5

History of DJing

1999: first DJ software
2006: harmonic mixing software

Mixxx software

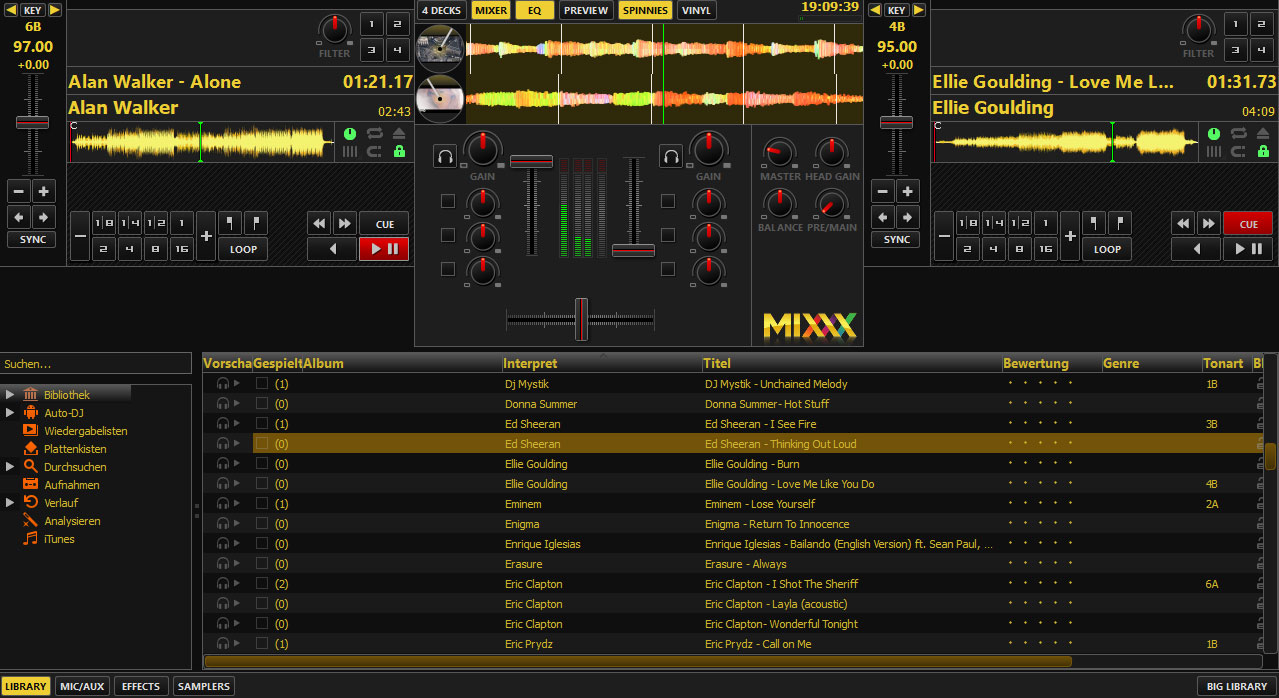
Noawadays, DJs do everything digitally. With the turn of the century, DJ software replaced the turntable and record collection. In modern DJ software, you can load a list of MP3 files, and using Feature Extraction, the software will automatically figure out the tempo and key information. When a track is playing, it can sort the list of tracks so that tracks with a tempo and key similar to the current track are shown on top.

In addition, the software can perform the beatmatching automatically. However, the harmonic mixing that my talk is about, is not yet included in current DJ software; at most the software allows you to pitch-shift a track up or down a key; any more advanced spectral modifications are still under research.

Image source: self-made screenshot of Mixxx, https://www.mixxx.org/

10.1

What is harmony?

Universal to all humans,

but varies based on personal experience

Before I can talk about harmonic mixing, I need to explain what harmony is. Harmony occurs when multiple tones are playing at the same time. Depending on the tones, this can either sound consonant (pleasant), or it can sound dissonant or very unpleasant to a human listener.

Harmony is mysterious in that it is universal to humans in all cultures, which led early people to believe that harmony was given to us by nature or a supernatural being.

But harmony also depends on the personal listening experience. When Western musicians first started clashing tones, only a few intervals were considered to be consonant, but over time, more and more intervals were added and as people became familiar with that music, they no longer considered those intervals to be dissonant.

This led to a crisis in the 20th century were composers feared that once the last remaining intervals were added (cf. atonal or twelve-tone music), music is finished, there would be no more room to expand. However, certain intervals have remained pretty dissonant no matter how often you hear them, suggesting that there is more to harmony than just familiarity.

10.2

Music theory

Consonant intervals:
octave, perfect fifth, major third

Dissonant intervals:
semitone, tritone

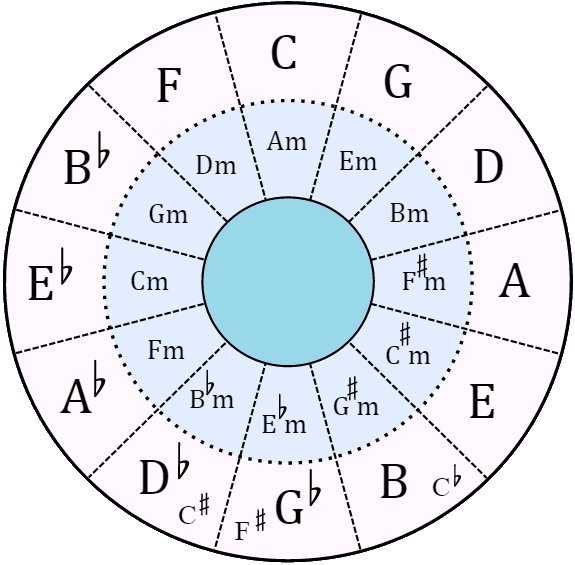
Circle of Fifths (Quintenzirkel)

In current music theory, the following intervals are considered to be very consonant: the unison, the octave, the perfect fifth, the perfect fourth and the major third. Dissonant intervals are the semitone, the tritone and the minor seventh.

A good tool for figuring out harmony is the Circle of Fifths, which you saw earlier. In the Circle of Fifths, the tones are ordered in a way that consonant intervals are close together, so e.g. going from a C, we know that E, F and G are very consonant because they are adjacent, while F# is dissonant because it is on the opposite end of the circle.

The Circle of Fifths works pretty well, and it is used in current DJ software but it is not very scientific. For our harmonic mixing, we need a better explanation for harmony.

Image source: http://www.fretjam.com/images/circle-of-fifths-simple.gif

10.5

Psychoacoustics

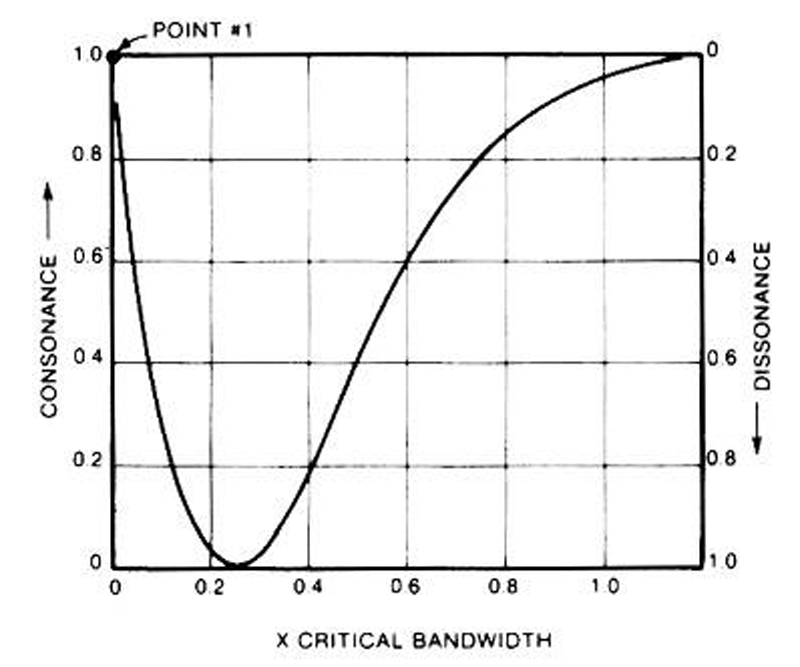
Roughness

Instead of music theory, we look at psychoacoustics. Psychoacoustics is the study of how music is picked up by the ears and how those audio signals are interpreted by the brain.

While the inner workings of the brain are not yet fully understood, there are some theories. The most promising theory is roughness, the psychoacoustic term for dissonance. The idea is that if two frequencies are too close together, our brain has difficulty differentiating between them, and this causes the unpleasant feeling.

In experiments from the 50s and 60s, the scientists figured out that if two frequencies are identical, the roughness is at zero but as you move the frequencies apart, the roughness increases. At one quarter of the critical bandwidth (CBW), the roughness is highest. If we move even further apart, the roughness decreases back to zero.

Image source: Vittorio Maffei's master thesis, page 48

10.4

Critical bandwidth

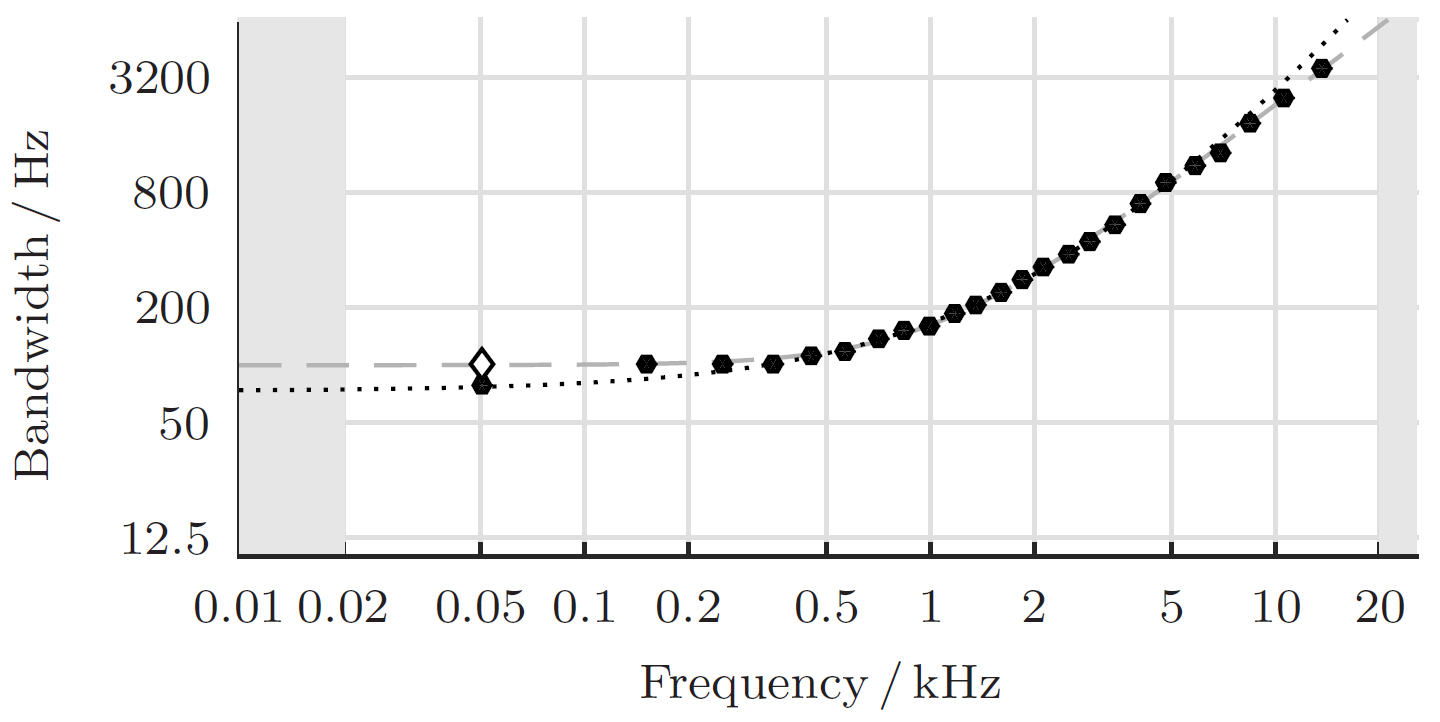
$$CBW(f) = 25 + 75 \cdot (1 + 1.4 \cdot (\frac{f}{1000})^2)^{0.69}$$

Zwicker (1961), Zwicker and Terhardt (1980)

You are probably not familiar with critical bandwidth; that's a term from psychoacoustics that describes the frequency resolution of our ear. In more experiments, the critical bandwidth was measured, and it changes based on the frequency.

Fortunately, being programmers, we do not have to worry about CBW too much, we just have to know that there is this function that approximates all the data points and we can now calculate the CBW given the frequency.

Image from Florian Völk: Updated analytical expressions for critical bandwidth and critical-band rate

10.6

Roughness

Given: $$f_1, f_2$$

$$\color{lime}{y} = \frac{\left|f_2 - f_1\right|}{CBW(\frac{f_1 + f_2}{2})}$$

$$Roughness(f_1, f_2) = max(\underbrace{(e^1 \cdot \frac{\color{lime}{y}}{0.25} \cdot e^{-\frac{\color{lime}{y}}{0.25}})^2}_{\color{gray}{= 16 y^2 \cdot e^{2-8y}}}, 0) \in [0, 1]$$

9.3

Harmonic series
(Naturtonreihe)

Fundamental frequency $$f$$

$$f, 2f, 3f, 4f, 5f, \ldots$$

9.2

Octave equivalence

$$\ldots \overset{\wedge}{=} A_4 \overset{\wedge}{=} A_5 \overset{\wedge}{=} A_6 \overset{\wedge}{=} \ldots$$

$$\ldots \overset{\wedge}{=} 440 Hz \overset{\wedge}{=} 880 Hz \overset{\wedge}{=} 1760 Hz \overset{\wedge}{=} \ldots$$

9.4

Tones and semitones

$$f + 2f + 3f + 4f + 5f + \ldots$$

$$f + \ldots + 1.25f + \ldots + 1.5f + \ldots + 1.75f + \ldots + 2f$$

12 semitones: A, A#, B, C, C#, D, D#, E, F, F#, G, G#

9.5

Tuning

Equal temperament (12-TET)
$$f_i = 440\ Hz \cdot 2^{\frac{i}{12}}, i \in \mathbb{Z}$$

Tone	$$A_4$$	$${A\sharp}_4$$	$$B_4$$	$$C_4$$	$${C\sharp}_4$$	$$D_4$$	$${D\sharp}_4$$	$$E_4$$	$$F_4$$	$${F\sharp}_4$$	$$G_4$$	$${G\sharp}_4$$	$$A_5$$
Hertz	440 = 440	466.16	493.88	523.25	554.37 ≈ 550	587.33	622.25	659.26 ≈ 660	698.46	739.99	783.99	830.61	880 = 880

All modern music follows the equal temperament tuning, and if we look at how the tones are mapped to frequencies, we find that 3rd harmonic (3f=1.5f) is mapped to the perfect fifth, and the 5th harmonic (5f=1.25f) is mapped to the major third.

In other words, everytime we play a single tone, we always get the major triad in the background, whether we want to or not. Therefore, the major triad will automatically sound very consonant because it amplifies the harmonics.

A tritone is one semitone below a perfect fifth. While this is outside of the critical bandwidth, once we look at the harmonic series, we can see what's going on. When playing e.g. C and F#, the third harmonic of C, which is G, will clash with F#: F# and G are at one quarter of the critical bandwidth. When we take all harmonics into account, not just the fundamental frequency, we can explain all dissonant intervals.

10.7

Roughness

Given two complex tones
$$\color{orange}{T_1 = \{(a_1, f_1), (a_2, f_2), (a_3, f_3), \dots \}},$$
$$\color{lime}{T_2 = \{(a_4, f_4), (a_5, f_5), (a_6, f_6), \dots \}}$$

$$Roughness(T_1, T_2) = \frac{\sum\limits_{\color{orange}{(a_i, f_i) \in T_1}} \sum\limits_{\color{lime}{(a_j, f_j) \in T_2}} \color{orange}{a_i} \cdot \color{lime}{a_j} \cdot Roughness(\color{orange}{f_i}, \color{lime}{f_j})}{\sum\limits_{\color{orange}{(a_i, f_i) \in T_1}} \sum\limits_{\color{lime}{(a_j, f_j) \in T_2}} \color{orange}{a_i} \cdot \color{lime}{a_j}} \color{gray}{\in [0, 1]}$$

11.1

Previous approaches

11.2

Key estimation

Before explaining what my chosen paper is all about, I'll give an overview of the previous approaches.

The first approach to harminc mixing was key estimation. Here, you look at the whole track, figure out the key based on the most common pitch (the tonic), and then use the circle of fifths to find a pitch shift so that the keys from both tracks will be very close together.

The problem with this approach is that it only works for tracks composed under the major-minor tonality, and it will fail for atonal or chromatic music. Since you just heard a full talk on key detection, I won't go into further detail.

11.3

Chroma based

Chroma-based approaches use a chromagram where the frequencies from a spectrum are mapped onto the 12 semitones from Western music. That way, you can see the most dominant notes over time, and can better figure out a pitch shift that sounds consonant.

The problem is that this approach expects a certain scale. If music uses e.g. 24 tones like in Asian music, or it follows a different tuning, then a tone may be put into a wrong bin, with bad results: If a track was detected incorrectly by just one semitone, the mixing will be off by one semitone, the most dissonant interval.
In the image, you can first see the original signal, then a chromagram, and then an averaged version of the chromagram.

Image source: Vittorio Maffei's master thesis, page 19

11.4

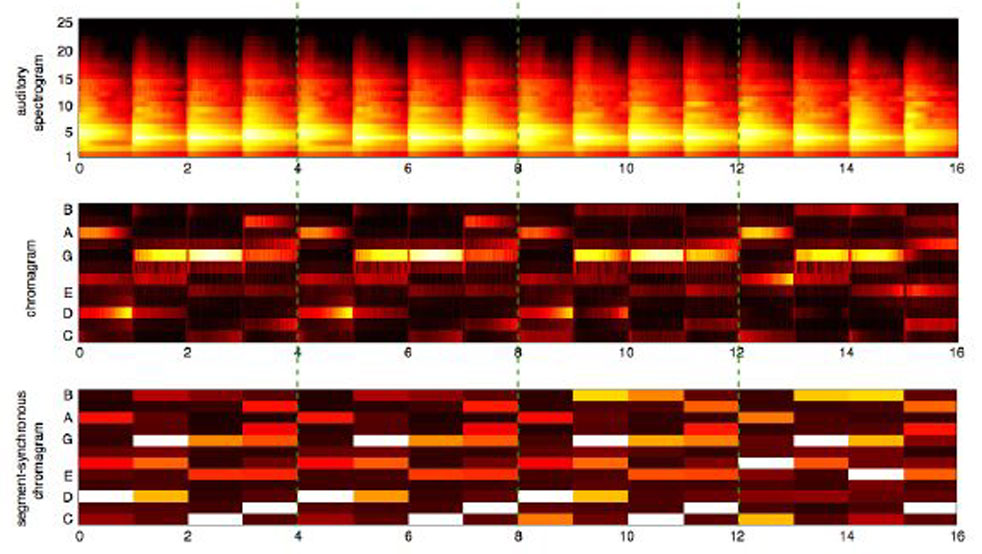
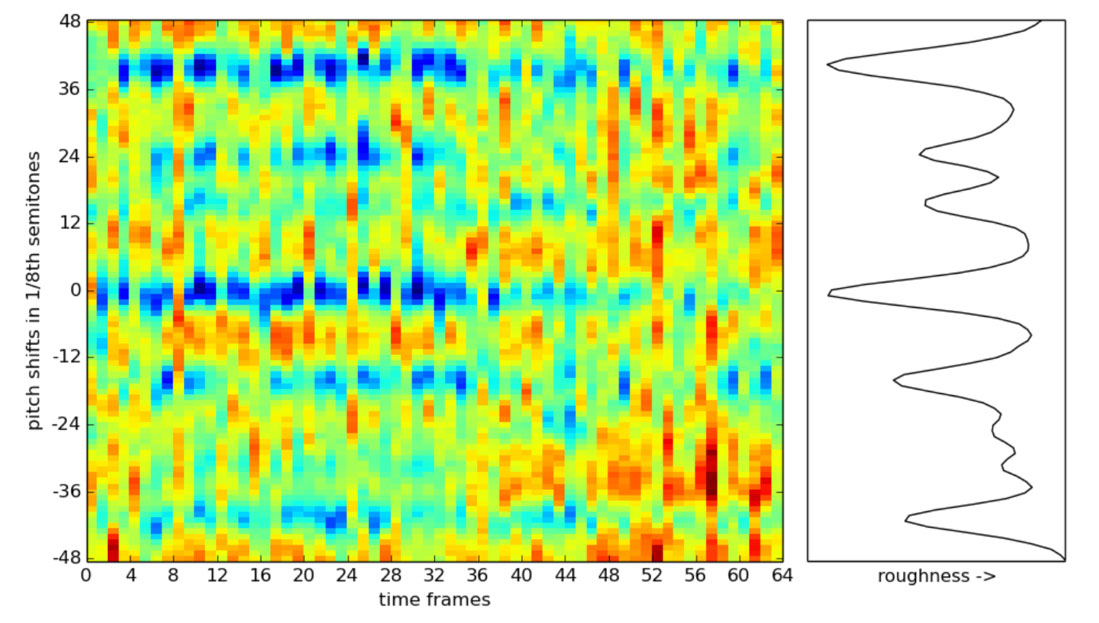
Roughness based

12.1

“Techniques for
automatic dissonance suppression
in harmonic mixing”

Master thesis by Vittorio Maffei (2014-2015)

12.2

12.3

Preprocessing

Tracks converted to mono, 44,100 Hz

Tempo changed to 120 bpm

8 second samples = 16 beats

12.4

Short time Fourier transform (STFT)

Blackman window

4096 window size, 256 hop size

4096 bins, 5000 Hz max frequency

→ 20 strongest partials extracted

12.5

Residual extraction

Split signal into sinusoids and residuals

Once he knows the strongest frequencies, the author subtracts them from the original signal. The idea is that these 20 partials contribute the most to the dissonance and should be modified, while the residual of the signal, which is mostly drums, bass and background noise, can be left unchanged.

The more we can leave unchanged, the better our final mix will sound because there is less chance for noise being added by our system. So following this step, we now have a sinusoid and residual signal for track 1.

Image source: Vittorio Maffei's master thesis, page 58

12.6

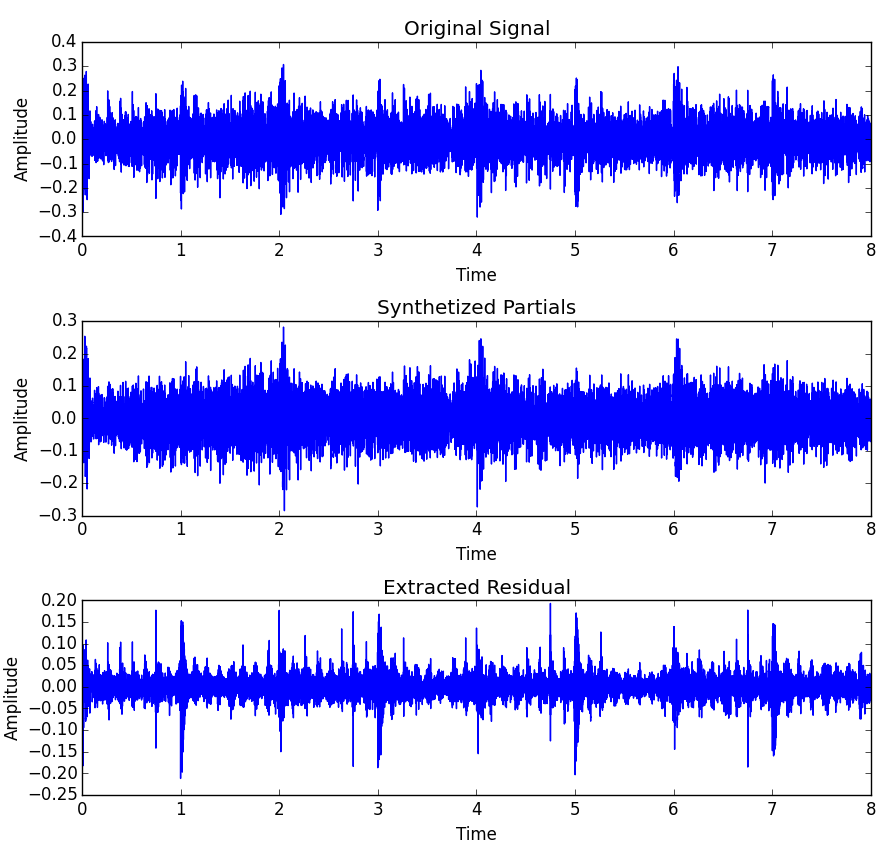
Temporal averaging

Averaged to 16^th notes

1379 windows → 64 windows

12.7

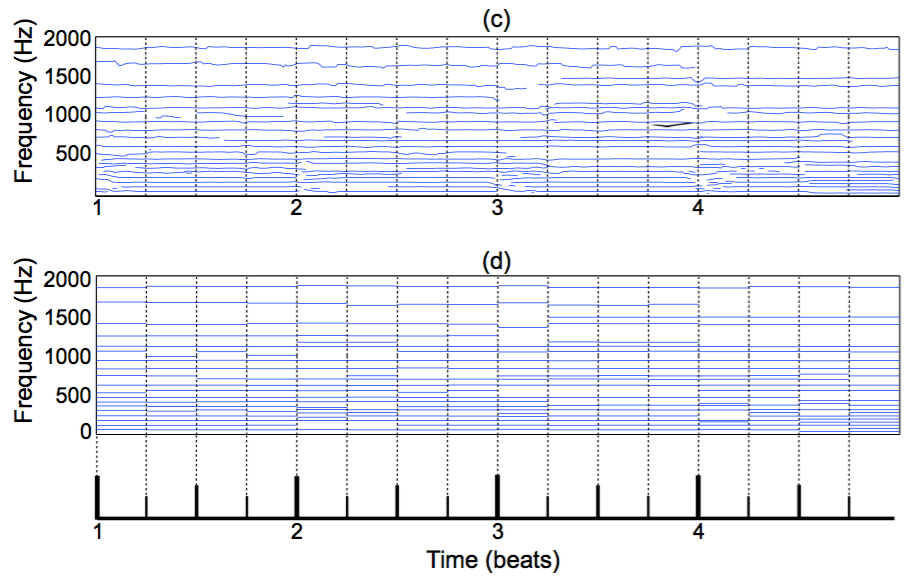
Optimal pitch-shift

12.8

Dissonance suppression

So far, everything was already included in the system by Gebhardt et al. What is new in Maffei's work is the dissonance suppression.

While we have performed a pitch-shift that minimizes the roughness, the roughness still varies over time. In certain time frames from the 8-second sample, the roughness will be higher than in other parts. So the author looked at the roughness measure over time and selected the most dissonant time frames, using a percentile approach.

First, he tried to silence the track during the roughest time frames but this resulted in very noticeable drops in volume, worse than by just keeping the dissonant parts in.

Image source: Vittorio Maffei's master thesis, page 65

12.9

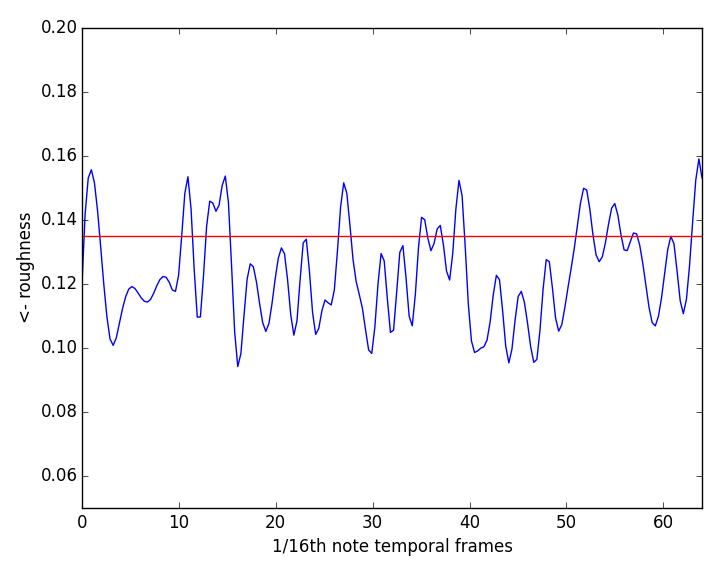
Partials suppression

Results

Improvements to disharmonic mixes
No changes to already harmonic mixes

The author asked 13 musically-trained listeners to rate the harmony in the samples from 1-6, both with his approach and with previous approaches. The result was that there were big improvements when mixes had dissonances under previous approaches, but there was not much change when the mixing was already pretty harmonic.

The samples shown are not from Maffei's work because he provided no samples, instead they are from Gebhardt et al. However, since both their systems are pretty similar, these samples can give us a hint on how harmonic mixing sounds like.

In the first row, you can listen to the original tracks. On the bottom-left, both tracks are mixed in their original form, while on the bottom-right, the tracks are mixed with a pitch-shift applied.

Audio samples taken from http://telecom.inesctec.pt/~mdavies/dafx15/

14.1

Criticism

Only tested on 8 second fragments
Only tested by musically trained listeners
No audio samples provided
Used existing libraries, did not build a new tool
Many typos

I enjoyed reading through the master thesis. Being written by a student and not by a professor, I found the text easy to understand; it was well explained and had a lot of detail.

Unfortunately, I found a lot of problems, both with this thesis and with harmonic mixing in general.

For example, I doubt that we can trust the results. In the end, we are looking for mixes in a club environment. If it takes musically trained listeners to figure out whether the mixing sounds pleasant or not, the average clubgoer, possibly drunk or drugged, will not notice much of a difference. Also, I question whether you can generalize the mixing based on just 8 second fragments.

Sadly, the author provided no samples, which makes it difficult to verify his work, and he built on existing work and used existing frameworks, there was not a lot of "new" research added by his thesis.

Finally, there are a lot of typos. While I can sympathize because he is not a native speaker, our professors always emphasize that we need to check for typos, so it is only fair to criticize typos in other people's work.

14.2

Future work?

Machine learning
Volume/loudness adjustment

For future improvements, the author only mentioned changing the parameters of his model, he didn't hint at other approaches.

In my opinion, machine learning should be investigated. So many research fields are getting better results by just throwing a neural network at the problem. I assume the same will be true for automatic mixing.

Also, volume/loudness adjustment could be added. I noticed this when listening to film music; there is a lot of variance between loud and quiet tracks. A good mix should adjust the volume to prevent quick changes in volume. This may not be a big issue for dance tracks though.

Obligatory Sources

Papers
- Vittorio Maffei: Techniques for automatic dissonance suppression in harmonic mixing. Master thesis at University of Milan, 2015.
- Richard Parncutt: Harmony: A Psychoacoustical Approach. Springer 1989.
- Florian Völk: Updated analytical expressions for critical bandwidth and critical-band rate. DAGA 2015, Nuremberg.
- Dave Cliff: Hang the DJ: Automatic Sequencing and Seamless Mixing of Dance-Music Tracks. HP Laboratories Bristol, 2000.
- Harmonic Keys magazine. 1986-1987.
Videos
- Howard Goodall: How Music Works. 4-part TV series on Channel 4 (UK), 2006.
- William Cox: Timeseries Data Superpowers: Intuitive Understanding of FIR Filtering and Fourier Transforms. OSCON 2014.
- Meinard Müller, Peter Grosche: Tempo and Beat Tracking. AudioLabs Erlangen, 2016.
- Tony Prince: The History of DJ. Video series by DMC.
- CD Projekt Red: The Witcher 3 : Wild Hunt. Music: General Approach. Wwise Tour 2016, Warsaw.
- PCDJ: various press videos from 2000
- Leonard Bernstein: The Unanswered Question. Lecture series at Harvard, 1973.
Websites
- Camelot Sound, company website.
- Web Audio API, MDN Web Docs.
For a complete list of sources, see the slide notes.

Takeaways

Roughness measure
(¼ of CBW = most dissonant)
Harmonic series
($f, 2f, 3f, \ldots$)

5 minutes of harmonic mixing (demo for Mixed in Key):

I hope that you will remember these two things:

1. With the roughness measure, we can calculate the dissonance of two tones. Two tones are dissonant if they are at one quarter of the critical bandwidth.

2. In nature, we never hear a single sinusoid tone, we always hear the harmonic series, which consists of the fundamental frequency f and its multiples.

Finally, you can listen to this mashup of harmonic mixing. It is originally an advertisement for the DJ software Mixed in Key. You can hear how the tempo and key stays constant throughout the mix. This sounds very boring because there is no chord progression that creates the forward progression in music that we know and love, but for mixing this is fine. If this were an hour-long mix, we'd find chord progressions inside each of the tracks, but for the handful of seconds where the mixing occurs, it is better to avoid dissonances.
Source: https://soundcloud.com/mixedinkey/shane-54-mixed-in-key-demo

Thanks for listening and I'm ready to answer any questions you might have.

Automatic mixing

Dissonance suppression during harmonic mixing

What is automatic mixing?

DJs in a club

History of DJing

History of DJing

History of DJing

History of DJing

What is harmony?

Music theory

Psychoacoustics

Critical bandwidth

Roughness

Harmonic series (Naturtonreihe)

Octave equivalence

Tones and semitones

Tuning

Roughness

Previous approaches

Key estimation

Chroma based

Roughness based

“Techniques forautomatic dissonance suppressionin harmonic mixing”

Preprocessing

Short time Fourier transform (STFT)

Residual extraction

Temporal averaging

Optimal pitch-shift

Dissonance suppression

Partials suppression

Results

Criticism

Future work?

Obligatory Sources

Takeaways

Harmonic series
(Naturtonreihe)

“Techniques for
automatic dissonance suppression
in harmonic mixing”